aulaCA008 - eletronica24h
Menu principal:
aulaCA008
Educacional > Cursos > Eletricidade em CA
Analise de Circuitos em Corrente Alternada
Aula 08: Circuito RC Serie
Bibliografia
Analise de Circuitos em Corrente Alternada - Saraiva/Erica
1 Circuito RC Série
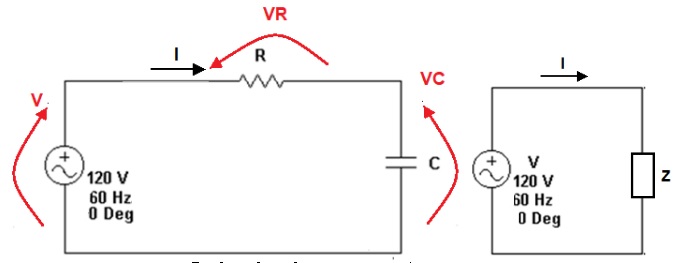
Como estudado em aulas anteriores, em um circuito puramente resistivo a tensão e a corrente estão em fase, e num circuito puramente capacitivo a corrente esta 90º adiantada em relação à tensão. Num circuito como o da Figura 1a a corrente continua na frente da tensão mas de um angulo menor do que 90º. O Diagrama Fasorial (D.F) resultante está representado na Figura 1b. Para construir o D.F é considerado, arbitrariamente, que a fase da corrente no circuito é 00 . Todos os outros fasores estarão atrelados a isso. Por exemplo, o fasor da tensão no capacitor estará atrasado de 900 em relação à corrente no circuito (que é a corrente no capacitor). E assim por diante. A Figura 1b mostra o DF construído.
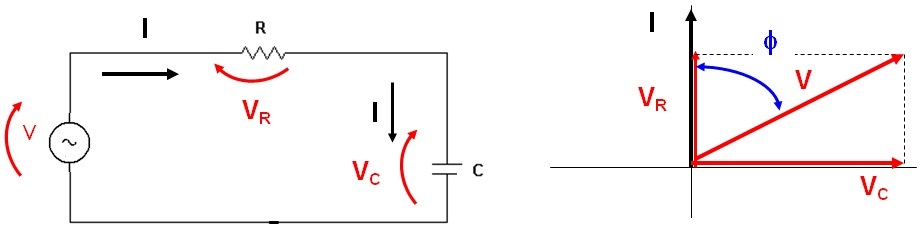
Figura 1 - Circuito RC serie ( a ) Circuito ( b ) Diagrama Fasorial
1.1 Triangulo das tensões
Na Figura 1b, existe um triangulo cujos lados são tensões, VR, VC e V chamado de Triangulo das Tensões, repetido na Figura 2 para maior compreensão.
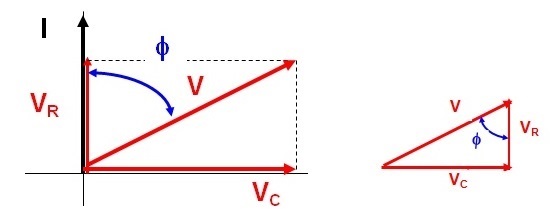
Figura 2 - O triangulo das tensões no circuito RC serie
A relação entre as tres tensões é dada pelo teorema de Pitagoras:
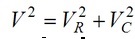
O angulo f é calculado por: f = arccos(VR/V)
1.2 Impedância capacitiva (ZC)
A oposição que um capacitor em serie com uma resistencia real oferece à passagem de uma corrente alternada é uma combinação da resistência ôhmica (R) com a reatância capacitiva (Xc) sendo chamada de impedância capacitiva (Zc). A impedancia Z é um numero complexo, pois é obtida dividindo a tensão pela corrente, ambas grandezas complexas.
Como associação é serie a oposição total equivalente, que é chamada de impedancia, Z, é a soma das oposiçoes resistiva, R, e reatancia capacitiva, isto é:
Z= R - jXc
Z= R - jXc
O modulo e a fase da impedancia podem ser obtidas do triangulo das impedancias o qual é obtido a partir do triangulo das tensões dividindo cada lado por I, Figura 3.
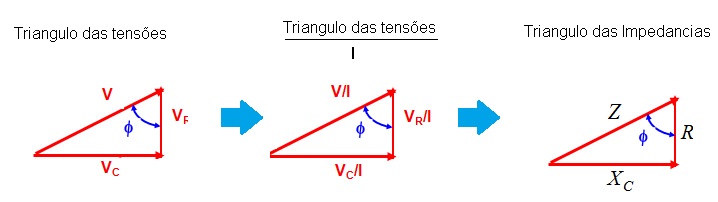
Figura 3 - Obtendo o Triangulo das impedancias
A relação entre Z, Xc e R é dada pelo teorema de Pitagoras:
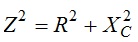
Z é o modulo da impedancia que determina o modulo da corrente (valor da corrente) que é medido pelo amperimetro.
I=V/Z isto é, o modulo da corrente é igual ao modulo da tensão dividido pelo modulo da impedancia.
I=V/Z isto é, o modulo da corrente é igual ao modulo da tensão dividido pelo modulo da impedancia.
A fase da impedancia f, e calculada por: f = arccos(R/Z), desta forma a impedancia pode ser escrita na forma polar e cartesiana.
Z= R - jXc forma cartesiana e
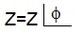 | é a impedancia na Forma polar |
1.3 Exercicio resolvido
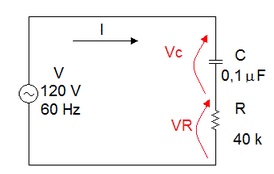
Solução:
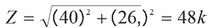
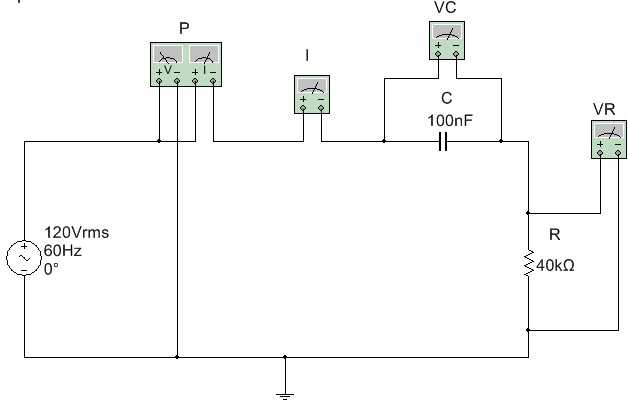
Para o circuito da Figura 4 calcule :
a) Impedância (Z)
b) Corrente (I)
c) Tensão em C e em R
d) Defasagem entre I e V.

Figura 4 - Circuito RC serie em CA - Exercicio
a) Primeiramente deveremos calcular a reatância do capacitor
Xc= 1/(2.p.60.0,1 mF) = 26.525 W Confira esse valor em Calculando Impedancia
Xc= 1/(2.p.60.0,1 mF) = 26.525 W Confira esse valor em Calculando Impedancia
A impedancia é calculada considerando o triangulo das impedancias
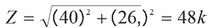
b) A corrente vale: I=V/Z = 120 V/ 48 k = 2,5 mA
c) A tensão no capacitor e resistor valem: Vc= Xc.I = 26,5 k x2,5 mA = 66,2 V VR=RxI = 40 k. 2,5 mA =100 V
d) cosf= R/Z = 40 k/48 k = 0,83= F.P e farccos0,83 = 33º
2 Experiencia: Circuito RC Série - Medida da corrente e tensões
2.1. Abra o arquivo ExpCA13_Circuito_RC_serie (Multisim 14) e identifique o circuito da Figura 5. Inicie a simulação e meça as tensões VR, VC e a corrente I. Meça tambem o fator de potencia e a potencia real (W) no Wattimetro. Anote esses valores na tabela 2.
Arquivo Multisim Live

Figura 5 - Circuito RC serie para experiencia
Tabela 2 - Valores medidos e calculados do circuito da Figura 5
| Valores Calculados | Valores Medidos por Simulação | ||||||||
| VR(V) | VC(V) | I(A) | P(W) | FP | VR(V) | VC(V) | I(A) | P(W) | FP |
2.2 No arquivo ExpCA13_Circuito_RC_serie (Multisim 14) identifique o circuito da Figura 6a. Inicie a simulação e abra o oscilocopio (ou o Grapher no Multisim Live).Posicione os dois cursores conforme Figura 6b e meça a defasagem no tempo indicada no osciloscopio (T2 - T1) ou no Grapher. Transforme para graus (não esqueça que a frequencia é 60 Hz que corresponde a um periodo T (16,666 ms) que por sua vez corresponde a 360 graus). Anote o valor da defasagem medida e a calculada.
f (calc)=______________ f (Med)=_______________
Obs: A precisão da medida depende da precisão da indicação dos cursores (deveria ser zero nos dois casos).
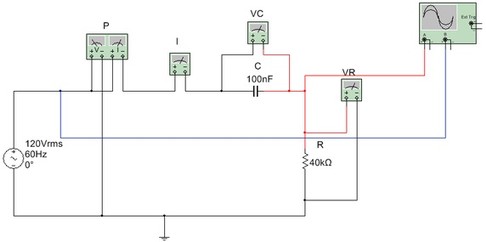
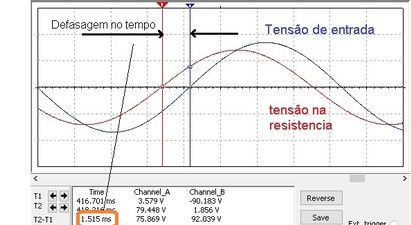
( a ) ( b )
Figura 6 - ( a ) Circuito para medir a defasagem ( b ) cursores posicionados para medir a defasagem
2.3. Compare os valores medidos e calculados.
2.4 Escreva as suas conclusões
3 Exercicios propostos
3.1 Qual a indicação de cada instrumento?
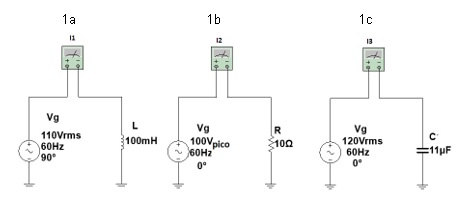
I1= I2= I3=
3.2 Desenhar o Diagrama Fasorial em cada circuito da questão 3.1
3.3 A impedância de um motor é dada por Z=3 + j4 (ohms). Determinar:
a) fator de potência do motor.
b) Valor da corrente se o mesmo for ligado em 220V
c) Ângulo de defasagem, em graus, entre a tensão e a corrente
3.4. A expressão em função do tempo de uma tensão é v(t)= 30.sen(377.t + 3)(V) sendo aplicada a um circuito e resultando a corrente i(t)=10.sen(377.t + 6)(A).
a) Qual o F.P do circuito?
b) Qual a expressão na forma complexa cartesiana da impedância do circuito?
3.5 Calcule a intensidade da corrente, o valor das tensões VR e VC e desenhe o diagrama fasorial . Considerar R=30k e C=100nF
3.6 Repita 3.5 se f=240 Hz